Note: This is a reprint of an article that originally appeared in the LA Times on April 8, 1999.

      What is all this fuss about spinning? As we have seen, a simple question such as “How do skaters get spinning so fast?” is not so simple. Many of you figured out that skaters bring their arms in to speed up, and this explains “how” but not “why.” So, this week, let’s take a look at “why!”

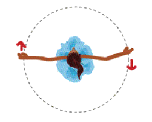      The top down views of the skater summarize what you found out. The first skater (right) has her arms extended and the short arrows indicate that she is spinning slowly.

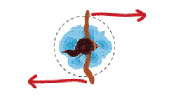
      When the same skater (as shown in the second drawing, below) holds her arms closer to her body, she spins faster, as indicated by the longer arrows. The arrows represent the “rotational velocity” with longer arrows representing a faster spin. Physicists use the symbol w for rotational velocity.

      What these diagrams show you is that the way the body is distributed has a large effect on the spinning speed. To describe this, physicists talk about something called “rotational inertia” and use the symbol I. Inertia is the tendency for a body to resist a change in motion. Spinning objects that are spread out will resist change more than compact objects. In other words, the more spread out an object is, the higher its rotational inertia. Objects that are more compact have low rotational inertia and are able to change more easily.

      When we combine rotational velocity and rotational inertia by multiplying them together (represented as Iw), we have defined angular momentum. Using this definition, we can show why skaters spin faster with their arms close to their bodies. As I mentioned in a previous article, the key to understanding the change in the skater’s speed is the Law of Conservation of Angular Momentum. An object’s angular momentum is conserved, unless an outside force acts on the object.

      Because of this conservation, if we change one part of angular momentum, the other part has to change. So, if the skater moves her arms closer to her body, both the rotational velocity and rotational inertia change, but in opposite directions.

      As the arms come in, rotational inertia decreases and rotational velocity increases, making the skater spin faster. But, if she puts her arms out, her rotational inertia increases, which decreases her rotational velocity and slows her down.

      So, now that you have an equation that describes how the skater controls spin, how can you apply this to the frozen fruit can experiment? Next week I will publish answers to that question, and you may be surprised. (I was!)