
Spin Lab
Geek Speak Notes
Richard Feynman is a Nobel prize-winning physicist who went to college at Massachusetts Institute of Technology. He challenged (and even annoyed) those around him to recognize their preconceptions (what they thought they knew) in order to "discover" new things that they couldn’t otherwise see.
In 1963, Feynman published the following notes (along with Robert Leighton and Matthew Sands, copyright California Institute of Technology):
On the Law of Conservation of Angular Momentum (Section 18-4):
If no external torques act upon a system of particles, the angular momentum remains constant.
A special case of great importance is that of a rigid body, that is, an object of a definite shape that is just turning around. Consider an object that is fixed in its geometrical dimensions, and which is rotating about a fixed axis. Various parts of the object bear the same relationship to one another at all times. Now let us try to find the total angular momentum of this object. If the mass of one of its particles is "m" and its position or location is at (x, y) then the problem is to find the angular momentum of that particle, because the total angular momentum is the sum of the angular momenta of all such particles in the body. For an object going around in a circle, the angular momentum, of course, is the mass times the velocity times the distance from the axis, and the velocity is equal to the angular velocity times the distance from the axis:

or, summing over all the particles "i" we get

where
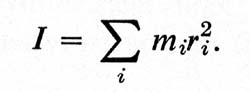
This is the analog of the law that the momentum is mass times velocity. Velocity is replaced by angular velocity, and we see that the mass is replaced by a new thing which we call the moment of inertia "I", which is analogous to the mass. The equations say that a body has inertia for turning which depends, not just on the masses, but on how far away the are from the axis. So, if we have two objects of the same mass, when we put the masses farther away from the axis, the inertia for turning will be higher.
There is one important difference between mass and moment of inertia which is very dramatic. The mass of an object never changes, but its moment of inertia can be changed. If we stand on a frictionless rotatable stand with our arms out stretched, and hold some weights in our hands as we rotate slowly, we may change our moment of inertia by drawing our arms in, but our mass does not change. When we do this, all kinds of wonderful things happen, because of the law of the conservation of angular momentum: If the external torque is zero, then the angular momentum (the moment of inertia times omega) remains constant. Initially, we were rotating with a large moment of inertia "I"; at a low angular velocity "w" and the angular momentum was "Iw". Then we changed our moment of inertia by pulling our arms in, say to a smaller value "I(2)". Then the product "Iw", which has to stay the same because the total angular momentum has to stay the same, was "I(2)w(2)". So "Iw=I(2)w(2)". That is, if we reduce the moment of inertia, we have to increase the angular velocity.